BiTree SearchBST(BiTree T,KeyType key){
//查找指针T所指二叉排序树中递归查找某个关键字等于Key的元素数据
//找到返回指向该元素结点的指针,否则返回空
if((!T) || EQ(key,T->data.key))return T;//查找结束
else if(LT(key,T->data.key))return SearchBST(T->lchild,key);
else return SearchBST(T->rchild,key);
}
Status SearchBST(BiTree T,KeyType key,BiTree f,BiTree &p){
//在T中查找key,查找成功P指向该元素节点,返回TURE,
//否则P指向查找路径的上访问的最后一个节点,并返回FLASE,指针f指向T的双亲,初始值为NULL
if(!T){
p=f;
return FALSE;
}else if EQ(key,T->data.key){
p=T;
return TRUE;
}else if LT(key,T->data.key){
return SearchBST(T->lchild,key,T,p);
}else return SearchBST(T->rchild,key,T,p);
}
Status InsertBST(BiTree &T,ElemType e){
//当二叉树T中不存在关键字等于e.key的数据元素时,插入e返回TRUE
BiTree p,s;
if(!SearchBST(T,e.key,NULL,p)){//查找失败
s = (BiTree)malloc(sizeof(BiTNode));
if(!s)exit(OVERFLOW);
s->data=e;
s->lchild=s->rchild=NULL;
if(!p)T=s;
else if LT(e.key,p->data.key)p->lchild=s;
else p->rchild=s;
return TRUE;
}
else return FALSE;
}
Status CreatBST(BiTree &T,int num,Status(* input)(ElemType &)){
//创建一个树
T = NULL;
ElemType e;
for(int i=0;i<num;++i){
input(e);
if(!InsertBST(T,e))printf("%3d %3d 创建失败! X\n",i+1,e.key);
else printf("%3d %3d 创建成功! V\n",i+1,e.key);
}
return TRUE;
}
Status PreOrderTraverse(BiTree T,Status(* Visit)(ElemType e)){
//中序遍历树
if(T){
if(PreOrderTraverse(T->lchild,Visit))
if(Visit(T->data))
if(PreOrderTraverse(T->rchild,Visit))return OK;
return ERROR;
}else return OK;
}
Status DeleteBST(BiTree &T, KeyType key){
//若存在key,删除该元素,返回TRUE 否则返回FALSE
if(!T)return FALSE;
else {
if(EQ(key,T->data.key))return Delete(T);//找到结点了,删除
else if(LT(key,T->data.key))return DeleteBST(T->lchild,key);
else return DeleteBST(T->rchild,key);
}
}
Status Delete(BiTree &p){
//再树中删除p并重新连接它的左右子树
BiTree q,s;
if(!p->rchild){//右子树为空 只需要重新连接左子树
q=p;
p=p->lchild;
free(q);
}else if(!p->lchild){//左子树空 连接右子树
q=p;
p=p->rchild;
free(q);
}else {//左右都不为空
q=p;
s=p->lchild;
while(s->rchild){
q=s;
s=s->rchild;//左转然后向右到尽头
}
p->data=s->data;//s指向被删结点的前驱
if(q!=p)q->rchild=s->lchild;//重连右子树
else q->lchild=s->lchild;//重连左子树
free(s);
}
return TRUE;
}
//查找指针T所指二叉排序树中递归查找某个关键字等于Key的元素数据
//找到返回指向该元素结点的指针,否则返回空
if((!T) || EQ(key,T->data.key))return T;//查找结束
else if(LT(key,T->data.key))return SearchBST(T->lchild,key);
else return SearchBST(T->rchild,key);
}
Status SearchBST(BiTree T,KeyType key,BiTree f,BiTree &p){
//在T中查找key,查找成功P指向该元素节点,返回TURE,
//否则P指向查找路径的上访问的最后一个节点,并返回FLASE,指针f指向T的双亲,初始值为NULL
if(!T){
p=f;
return FALSE;
}else if EQ(key,T->data.key){
p=T;
return TRUE;
}else if LT(key,T->data.key){
return SearchBST(T->lchild,key,T,p);
}else return SearchBST(T->rchild,key,T,p);
}
Status InsertBST(BiTree &T,ElemType e){
//当二叉树T中不存在关键字等于e.key的数据元素时,插入e返回TRUE
BiTree p,s;
if(!SearchBST(T,e.key,NULL,p)){//查找失败
s = (BiTree)malloc(sizeof(BiTNode));
if(!s)exit(OVERFLOW);
s->data=e;
s->lchild=s->rchild=NULL;
if(!p)T=s;
else if LT(e.key,p->data.key)p->lchild=s;
else p->rchild=s;
return TRUE;
}
else return FALSE;
}
Status CreatBST(BiTree &T,int num,Status(* input)(ElemType &)){
//创建一个树
T = NULL;
ElemType e;
for(int i=0;i<num;++i){
input(e);
if(!InsertBST(T,e))printf("%3d %3d 创建失败! X\n",i+1,e.key);
else printf("%3d %3d 创建成功! V\n",i+1,e.key);
}
return TRUE;
}
Status PreOrderTraverse(BiTree T,Status(* Visit)(ElemType e)){
//中序遍历树
if(T){
if(PreOrderTraverse(T->lchild,Visit))
if(Visit(T->data))
if(PreOrderTraverse(T->rchild,Visit))return OK;
return ERROR;
}else return OK;
}
Status DeleteBST(BiTree &T, KeyType key){
//若存在key,删除该元素,返回TRUE 否则返回FALSE
if(!T)return FALSE;
else {
if(EQ(key,T->data.key))return Delete(T);//找到结点了,删除
else if(LT(key,T->data.key))return DeleteBST(T->lchild,key);
else return DeleteBST(T->rchild,key);
}
}
Status Delete(BiTree &p){
//再树中删除p并重新连接它的左右子树
BiTree q,s;
if(!p->rchild){//右子树为空 只需要重新连接左子树
q=p;
p=p->lchild;
free(q);
}else if(!p->lchild){//左子树空 连接右子树
q=p;
p=p->rchild;
free(q);
}else {//左右都不为空
q=p;
s=p->lchild;
while(s->rchild){
q=s;
s=s->rchild;//左转然后向右到尽头
}
p->data=s->data;//s指向被删结点的前驱
if(q!=p)q->rchild=s->lchild;//重连右子树
else q->lchild=s->lchild;//重连左子树
free(s);
}
return TRUE;
}

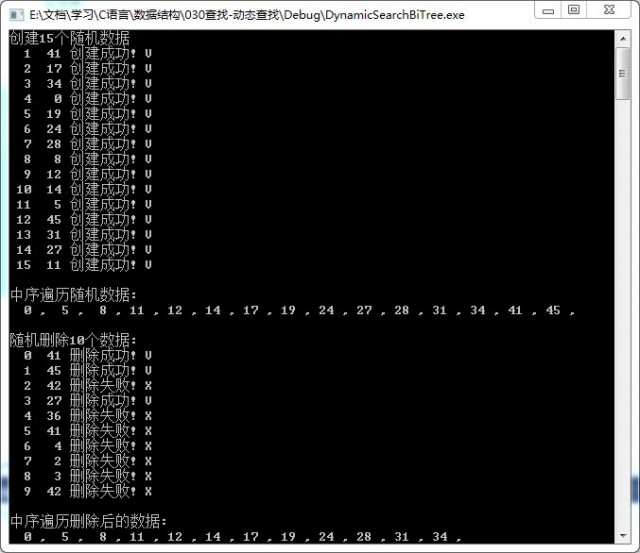
如此与时俱进,让人佩服
正在学这个而已!